Linear regression and correlation analysis
•第五章中,我们介绍了如何研究两个定性变量是否有关系的问题。
•实际工作中,我们经常需要研究两个或两个以上定量变量是否有关系,有怎么样的关系。
•对于生物学数据,因为存在随机性和变异性等,所以通常不能推导出确定的函数关系,但是可以使用统计学上的回归与相关分析研究其分布情况(如平均数、标准差和置信区间)。
因果关系与平行关系
•经常地,我们发现一个变量随着另一个变量的变化而变化,但是这不一定说明两者存在因果关系。
•还有一种可能是这两者共同受到另外一个变量的影响,称为平行关系。
散点图(scatter chart):直观的查看x、y的关系。
两个变量间关系的性质和程度;
两个变量间关系的类型,是直线型或者曲线型。
是否有异常观测值的干扰
==回归分析==(regression analysis):回归分析经常用于研究两个变量的因果关系,建立回归方程用于根据自变量==预测==和==控制==因变量。
表示原因的变量称为自变量(independent variable),常用x表示,一般是试验中预先确定的,没有随机误差。
表示结果的变量称为因变量(dependent variable),常用y表示,y随x的变化而变化,且具有随机误差。
| 回归分析的分类 | |
|---|---|
| 根据自变量,因变量的数目 | 一个自变量与一个因变量:一元回归分析 |
| 多个自变量与一个因变量:多元回归分析 | |
| 根据变量间关系的类型 | 直线回归(linear regression) |
| 曲线回归(curve regression) |
相关分析(correlation analysis):相关分析通常用于研究两个变量的平行关系。变量x和y无自变量和因变量之分,且都具有随机误差。
| 相关分析的分类 | |
|---|---|
| 对两个变量之间的直线关系进行相关分析 | 直线相关(linear correlation)分析或简单相关(simple correlation)分析 |
| 一个变量与多个变量的线性相关 | 复(multiple)相关分析 |
| 保持其余变量不变的情况下研究两个变量的线性相关 | 偏(partitial)相关分析 |
直线回归
直线回归的数学模型
虽然x固定时,y并没有确定的值,但是此时y的分布是固定的,或者说其平均数等指标是固定的。
$$
\mu_Y=\alpha+\beta X
$$
$\alpha$为直线在y轴的截距(intercept)
$\beta$为直线的斜率(slope)
$$
Y=\alpha+\beta X+\epsilon
$$
若使用样本资料估计参数
$$
y=a+bx+e
$$
==直线回归方程的参数估计==
$$
b=\frac{\sum (x-\overline x)-(y-\overline y)}
{\sum(x-\overline x)^2}
=\frac{SP}{SS_x}
$$
b的分子简称为两个离均差的乘积和,记作SP或$SS_{xy}$
b的分母称为离均差平方和,记作$SS_x$
$\alpha=\overline y-b\overline x$
回归方程的三个基本性质
(1)$Q=\sum(y-\hat y)^2$最小
(2)$\sum(y-\hat y)=\sum(y-a-bx)=0$
(3)$\hat y=\overline y-b\overline x+bx=\overline y+b(x-\overline x)$即直线通过中心点$(\overline x,\overline y)$
注意:直线回归方程的适用范围不能超过计算时用到的x的范围;不是所有的散点都落在回归直线上,但是很接近回归直线。
直线回归的假设检验
直线回归必须检验,F检验和t检验都可以用于直线回归的假设检验
•根据方差分解的思想,我们也可以把y的总方差分解成,x引起的y的方差(称==回归方差==)和随机方差(称==离回归方差==)两部分。
如果回归方差显著大于离回归方差,那么说明x对y的影响大于随机误差,即y对x的回归关系是显著的,否则则说明回归关系不是显著的。
直线回归的平方和分解
$$
\sum(y-\overline y)^2=\sum(\hat y-\overline y)^2+\sum(y-\hat y)^2\
左边y的离均差平方和,也称为总平方和SS_y\
第一项称回归平方和,记作U或SS_{回归}\
第二项称为离回归平方和,也称残差平方和(剩余平方和),记作Q,SS {离回归}或SS{剩余}
$$
$$
U=\sum(\hat y-\overline y)^2\
=b^2\sum(x-\overline x)^2=b^2SS_x=\frac{SP^2}{SS_x}\
Q=SS_y-U
$$
直线回归的自由度分解
总自由度为n-1
一元直线回归,只涉及到一个自变量,所以回归平方和的自由度为1
离回归平方和的自由度等于以上两者之差n-2
直线回归的F检验
因为方差等于平方和除以自由度:
$$
S^2_{回归}=\frac{U}{1}\
S^2_{离回归}=\frac{Q}{n-2}\
F=\frac{S^2_{回归}}{S^2_{离回归}}\
若F值落在F分布的右尾拒绝区,则说明直线回归关系显著
$$
直线回归的t检验
$Y=\alpha+\beta X+\epsilon$
$\beta$等于零,那么y与x就没有关系
b的平均数是$\beta$
$$
S_b=\frac{S_{离回归}}{\sqrt{SS_x}}\
t=\frac{b-\beta}{S_b}=\frac{b}{S_b}
(假设\beta=0)
$$
若t落在$df=n-2$的t分布的双尾拒绝区内说明$\beta$与0的差异显著,即直线回归关系显著。
F检验和t检验的本质完全相同。
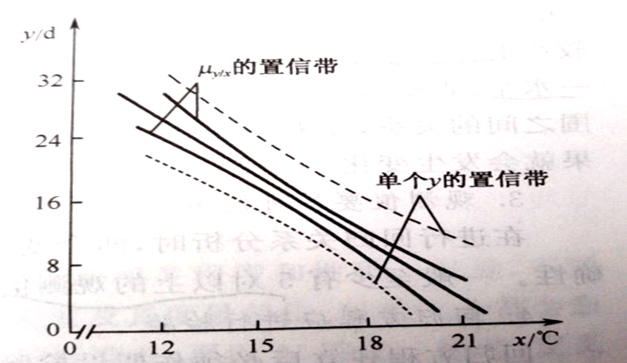
1.回归直线位于$\mu_{y/x}$的置信区间的中间。
2.$\mu_{y/x}$的置信区间位于y置信区间的中间。
3.随着x远离平均数时,置信区间越宽,即回归直线描述数据关系的适合度变差
直线回归的应用注意
•1. 描述两个变量的依存关系。
•2. 在一定范围内,根据自变量对因变量进行预测。
•3. 通过控制自变量来控制因变量。
PS:要符合生物学意义,区分自变量和因变量,==必须检验==,外推要谨慎。
直线相关
•如果不需要区分自变量和因变量,只想了解两个变量的相关程度(degree of correlation)和相关性质(character of correlation),则可以是使用==相关系数==(correlation coefficient)来描述。
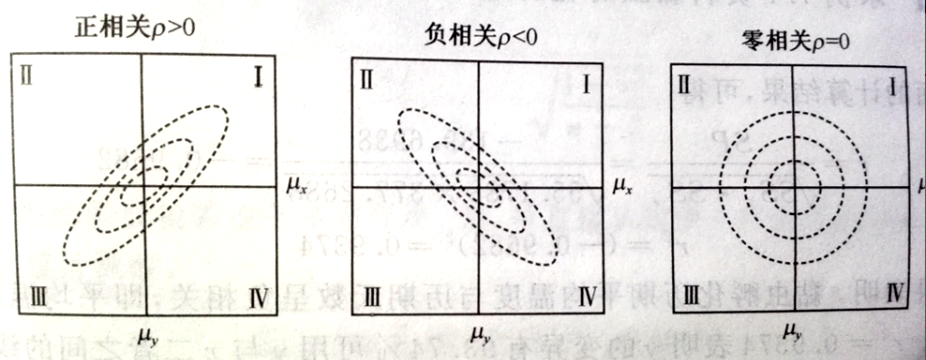
相关系数
若使用样本资料时
$$
r=\frac{\sum(x-\overline x)(y-\overline y)}
{\sqrt{\sum(x-\overline x)^2\sum(y-\overline y)^2}}
=\frac{SP}{\sqrt{SS_xSS_y}}
=\sqrt{\frac{U}{SS_y}}
$$
计算相关系数时,两个变量是平等的,不区分自变量和因变量,这是相关和回归的主要区别。
相关系数的是指就是回归平方和与总平方和比率的平方根,所以==取值范围为[-1,1]==。
决定系数
$$
r^2=\frac{SP^2}{SS_xSS_y}
=\frac{U}{SS_y}
$$
决定系数的含义是回归平方和占总平方和的比率,取值范围[0,1]。
直线相关的相关系数假设检验
计算出相关系数以后,并不能说明两者真的相关,还必须使用假设检验来推断,根据样本资料计算的r的理论值ρ与0的差异是否显著。
$$
S_r=\sqrt{\frac{1-r^2}{n-2}}\
t=\frac{r-\rho}{S_r}
=\frac{r}{S_r}
$$
如果t值落在$df=n-2$的t分布的拒绝区,才说明相关是显著的。
•相关显著性检验的$t_r$与回归显著性检验的$t_b$是相等的,所以两个变量的回归系数和相关系数的t检验本质是完全相同的。
r临界值表,查询附表8,可以发现随着df的增大,r的临界值变小,也就是说为了发现弱相关性,必须样本足够大才行。
直线相关的应用注意
•1. 两个变量应该都服从正态分布。
•2. 相关系数必须进行检验。
•3. 变量应尽可能多。
•4. 相关系数显著说明两个变量之间存在相关性,到底是因果关系还是平行关系要根据生物学知识进行判断。
总结
==直线回归和直线相关有什么区别?==
直线回归需要区别自变量和因变量,自变量一般是代表原因的量,或者是可以严格控制的量,因变量应服从正态分布;直线相关则要求两者都服从正态分布,两者的地位是完全相同的。
直线回归一般用于研究因果关系,而直线相关一般用于研究平行关系。
回归系数b取值范围是负无穷到正无穷,而相关系数r的取值范围是[-1,1]。
b越大,说明直线的斜率越大;|r|越大,说明散点距离直线越近,或者说直线方程的拟合程度越好。
==•直线回归和直线相关有什么联系?==
•1. r和b的正负号一定是相同的。
•2. 假设检验是等价的。
•3. 直线回归的F检验过程中要计算总平方和和回归平方和,而$r^2$则是回归平方和与总平方和的比值。
•4. 若x和y均为正态分布时,也可以分别计算以x为自变量的回归系数,和以y为自变量的回归系数,且$r^2=b_{x/y}b_{y/x}$。

