Biostatistics生物统计学第六讲方差分析

---

第六讲 方差分析

第四章介绍了如何比较样本平均数与参考总体平均数，以及比较两个样本平均数。但如果有三个或更多的样本平均数

有三个或更多的样本平均数时，u检验/t检验都有一定的局限，不适用

本文有些数学公式使用md语法打的，刚学这个，有的嫌太累了😂直接用的图片

第一节 方差分析

•方差分析(analysis of variance，ANOVA)又称变量分析，是把所有分组的观测值作为==一个整体==，一次性比较各组的样本平均数并做出推断。

•如果差异不显著，则认为各组都是相同的；如果差异显著，再进一步比较是哪组数据与其他数据不同。

因素factor	试验中所研究的影响试验指标的原因或原因组合。温度，湿度
水平level	每个因素的不同状态，温度（20℃、30℃、40℃）
处理treatment	对受试对象给予的某种外部干预，2种温度+3种湿度=6种处理
重复repetition	在试验中，将同一种重复实施在不止一个实验单位上
效应effect	试验因素相对独立的作用，正效应/负效应
互作interaction	两个或两个以上处理因素间相互作用所产生的效应

方差分析的基本思想
造成观测值发生不同的原因可以分为两大类
一类是**处理效应(treatment effect)**，是试验中对不同个体给予不同处理引起的
二类是**误差效应(error effect)**，是试验中偶然性因素的干扰和测量误差所致
方差分析就是把所有观测值的==总方差分解成处理方差和误差方差并相互比较==，看处理效应是否显著大于误差效应

---

方差分析的观测值和平均数

•如表，某试验有k个处理组，且每处理重复n次。

•那么可以计算出每组观测值的平均数$x_i$.，和所有观测的平均数$\overline{x_{..}}$。

---

方差分析的线性模型

每一项观测值：
$$
x_{ij}=\mu+T_i+\epsilon_{ij}
$$

如果用样本来估计参数:
$$
x_{ij}=\overline{x_{..}}+t_i+e_{ij}
$$

---

处理效应的三种模型

1. 固定模型(fixed model)：各个处理的效应是特异选择的可以人为控制的固定常量，是由固定因素引起的，且这些常量的和为0
2. 随机模型(random model)：各个处理的效应不是常量，而是由随机因素所引起的随机变量，且这些变量服从正态分布N(0, $σ^2$)
3. 混合模型(mixed model)：在多因素试验中，既包括固定效应的试验因素，又包括随机效应的试验因素
三种模型的差异：平方和和自由度的计算是相同的，但统计数F的计算公式是不同的，对试验的设计和结果的解释也存在不同。
固定模型侧重于效应值的估计和比较，而随机模型侧重于效应值的变异程度的估计和检验。
对于单因素方差分析，因为不存在互作，固定模型和随机模型没有区别

---

方差分析的三大步骤：

1. 计算方差**(==平方和分解==和==自由度分解==)。**	$s^2=\frac{\sum(x_i-\overline{x})^2}{n-1}$计算离均差平方和，计算自由度，最后相除得方差	方差就是离均差平方和除以==自由度==。|
2. 计算统计数F。	$F=\frac{S^2_t}{S^2_e}$
3. (若F检验结论是差异显著)多重比较。

平方和分解

$$
K个组的数据累加，
\\sum_{i=1}^k\sum_{j=1}^n(x_{ij}-\overline{x_{..}})^2
=\sum_{i=1}^k\sum_{j=1}^n(x_{ij}-\overline{x_{i.}})^2
+n\sum_{i=1}^k(\overline{x_{i.}}-\overline{x_{..}})^2
$$

•上面等式左边项称为==总平方和$SS_T$==，反映所有数据距离总平均数的变异情况。

•右边第一项称为==组内平方和$SS_e$==，反映每组内部数据距离本组平均数的变异情况。

•右边第二项称为==组间平方和$SS_t$==，反映每组的组平均数距离总平均数的变异情况。
$$
令常数C=\frac{T^2}{nk},\
SS_T=\sum^k_{i=1}\sum^n_{j=1}x_{ij}^2-C\
SS_t=\frac{1}{n}\sum^k_{i=1}T_{i.}-C\
SS_e=SS_T-SS_t
$$
$SS_T$就是所有观测值的平方的累加减去常数C；

$SS_t$就是每组观测值和的平方的累加除以n再减去常数C

自由度分解

•k个分组，每组n次重复，总共$n_k$个观测值；

•总自由度$df_T=n_k-1$

•组间自由度$df_t=k-1$

•组内自由度$df_e=k(n-1)=df_T-df_t$

计算方差

$$
S^2_t=\frac{SS_t}{df_t}\
S^2_e=\frac{SS_e}{df_e}
$$

F检验

$$
F=
\frac{S^2_t}{S^2_e}
$$

•如果组间的总体方差等于组内的总体方差，那么上式就会落入F分布大概率区间内，如果落在小概率区间内，则认为假设不成立，即两个总体的方差不相等。

•方差分析时的F检验只有右尾检验，如果落入右尾拒绝区，说明处理效应显著大于误差效应，即组间有显著差别。

多重比较

•如果F检验否定了零假设，说明k个处理的平均数之间有显著差异，但并不意味着每两个处理的平均数间的差异都是显著的，也无法分别具体是哪些平均数间的差异是显著的。

•因此，就要进行多重比较。

最小显著差数法LSD法
标记字母法	不建议使用
梯形表示法	建议使用

最小显著极值法LSR法
新复极差检验(SSR法)
q检验(SNK法)

最小显著差数法

•统计学家Fisher最早提出了最小显著差数法，又称LSD法，其实质就是两个平均数相比较的t检验法。

•先计算出达到差异显著的最小差数，记为LSD，然后比较两个处理平均数的差值与LSD，如差值大于LSD，即认为差异显著。
$$
LSD_{0.05}=t_{o.o5}\cdot s_{\overline{x_1}-\overline{x_2}}\
LSD_{0.01}=t_{0.01}\cdot s_{\overline{x_1}-\overline{x_2}}\
其中s_{\overline{x_1}-\overline{x_2}}
=\sqrt{S^2_e(\frac{1}{n_1}+\frac{1}{n_2})}\
t_{0.05}是自由度为df_e的t检验临界值\
若|\overline{x_1}-\overline{x_2}|>LSD_{0.05},即为两者差异显著；\
若|\overline{x_1}-\overline{x_2}|>LSD_{0.01},即为两者差异极显著；
$$

标记字母法

•1. 把全部平均数从大到小依次排列；

•2. 在最大的平均数后标上a，然后依次向下比较，若不显著则也标上a，若遇到第一个显著则标上b，并停止比较。

•3. 以标有b的平均数为标准，依次向上比较，若不显著则在a的后面再加上b，直到遇见第一个显著时不做任何标记，并停止比较。

•4. 以标有b的最大平均数为标准，依次向下比较，若不显著则也标上b，若遇到第一个显著则标上c，并停止比较。

•5. 以此类推，反复进行，直到所有平均数都被标记了字母为止。

梯形表示法

•使用三角形阵列的格式展示出所有平均数差值，把各差值与LSD相比，*代表大于$LSD_{0.05}$，**代表大于$LSD_{0.01}$。

•结论：

•A1与A2和A4差异极显著，A1与A3差异显著；

•A3与A4差异极显著，A2与A4差异也极显著；

•A2和A3差异不显著。

==LSD方法的局限==

•LSD法的优点是比较简单，相对于t检验的优势是 把组内方差作为各组统一的试验误差。

•但是，仍有推断可靠性低，犯α错误概率增加的问题。

•多个处理平均数相互比较时，处理水平差异不同时，显著性阈值取相同标准不合理，应该做出适当调整。

最小显著极值法

•最小显著极差法(LSR法)是在比较多个处理的数据时，根据处理平均数在按大小排序时的距离的不同，而采用不同的显著差数标准。

SSR法

•1. 在各样本容量相等时，计算平均数标准误：
$$
S_{\overline{x}}=\sqrt{\frac{S^2_e}{n}}\
$$
•2. 查附表6中的SSR值，再计算最小显著差值：
$$
LSR_{\alpha}=SSR_{\alpha}\cdot s_{\overline{x}}
$$
•SSR表有两个参数，一个是自由度，另一个是M值，M值表示按大小排列时的距离，两者相邻记为2，中间隔一个记为3，以此类推。

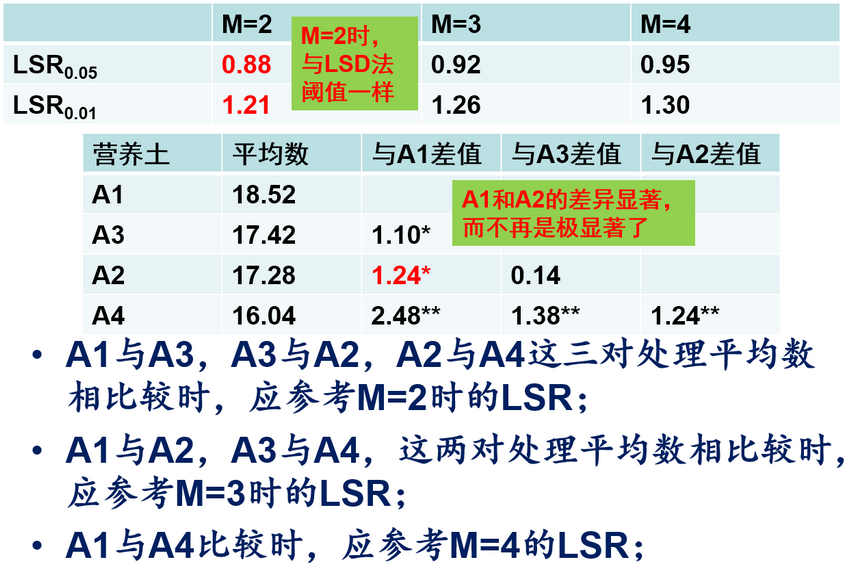
q检验

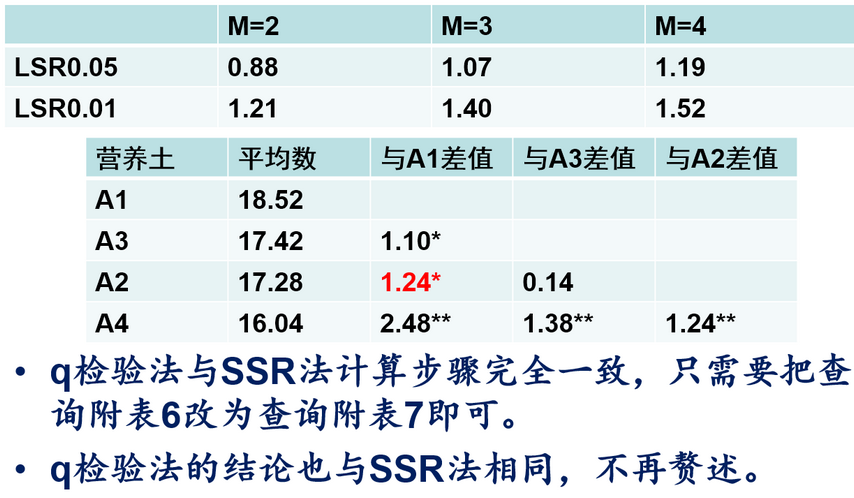
多重比较的三种方法选择

•M=2时，三种方法的显著性阈值相同；但M>2时，LSD法的显著性阈值最小，而q检验法的显著性阈值最大。

•结论：

•当处理数为2时，三种方法结论一致；

•当处理数增加时，==LSD法最灵敏(sensitive)==，==q检验法最保守(conservative)==。

•因为α错误和β错误是此消彼长的关系，不可能同时下降，==最容易犯α错误的是LSD法==，而==最容易犯β错误的是q检验法==，所以根据不同试验中两种错误的重要性不同来选择不同方法。

第二节 单因素(single factor)方差分析

1.当各处理重复次数相等时，方差分析的步骤就是计算出下表中的各值，然后与附表5比较。

	$df$	$SS$	$S^2$	$F$
处理间	k-1	$SS_t=\frac{1}{n}\sum_{i=1}^kT_{i.}^2-C$	$S_t^2=\frac{SS_t}{df_t}$	$\frac{S_t^2}{S_e^2}$
处理内	k(n-1)	$SS_e=SS_T-SS_t$	$S_e^2=\frac{SS_e}{df_e}$
总	nk-1	$SS_T=\sum_{i=1}^{k}\sum_{j=1}^nx_{ij}^2-C$

2.组内重复次数不相等时

组内重复次数不相等时，仍然可以使用方差分析，不过计算公式稍有变化。•组内重复次数不相等的试验要尽量避免，因为这样的试验数据不仅计算麻烦，而且降低了分析的灵敏度。

第三节 二因素方差分析

•对于有两个因素的试验，除了分析各因素的处理效应外，还需要考虑到因素间的互作效应。

•当互作效应非常大时，甚至可以忽略主效应。

•是否存在互作可以根据统计方法判断，也可以根据专业知识判断。

•只有每个处理都有重复的情况下，才能用统计方法分析互作效应。

处理无重复时

•按照方差分析的思想，可以把所有观测值的方差分解成处理A效应方差、处理B效应方差和误差效应方差并相互比较。

处理有重复时

•如果A因素有a个水平，B因素有b个水平，且每个处理组合重复n次时，则A因素的每个水平总共有bn个重复，而B因素的每个水平总共有an个重复，总共有abn个观测值。

平方和分解

$$
C=\frac{T^2}{abn}
$$

自由度分解

•总自由度$df_T=abn-1$

•因素A自由度$df_A=a-1$

•因素B自由度$df_B=b-1$

•AB互作自由度$df_{AB}=(a-1)(b-1)$

•组内随机误差自由度$df_e=ab(n-1)$

计算方差

$$
S^2_A=\frac{SS_A}{df_A}\
S^2_B=\frac{SS_B}{df_B}\
S^2_{AB}=\frac{SS_{AB}}{df_{AB}}\
S^2_e=\frac{SS_e}{df_e}
$$

F检验

•对于AB互作效应：
$$
F_{AB}=\frac{S^2_{AB}}{S^2_e}
$$
•若A或B为固定因素时：
$$
F_A=\frac{S^2_{A}}{S^2_e}
,
F_B=\frac{S^2_{B}}{S^2_e}
$$
•若A或B为随机因素时：
$$
F_A=\frac{S^2_{A}}{S^2_{AB}}
,
F_B=\frac{S^2_{B}}{S^2_{AB}}
$$

二因素方差分析总结

具重复观测值得二因素资料方差分析表

变异来源	$SS$	$df$	$s^2$
因素A	$SS_A$	$a-1$	$s^2_A$
因素B	$SS_B$	$b-1$	$s^2_B$
$A\times B$	$SS_{AB}$	$(a-1)(b-1)$	$s^2_{AB}$
误差	$SS_e$	$ab(n-1)$	$s^2_e$
总变异	$SS_T$	$abn-1$

第四节 多因素方差分析

•其实就是把二因素方差分析扩展到一般情况。

•此时，总方差可以分解成各因素的主效应误差，因素两两之间的互作效应误差，因素三三之间的互作效应误差，……，以及随机误差。

第六节 方差分析应满足的三个条件

•1. 可加性。处理效应与误差效应是可加的。

•2. 正态性。试验误差应当服从正态分布N(0，$σ^2$)，也就是说被检验的每一个总体都是正态分布。

•3. 方差齐性。各处理的误差方差均为$σ^2$。

•以上三个条件中，影响最大的是方差齐性，因此在做方差分析前应该先进行方差齐性检验。